控制包示例¶
下面是一些综合性的教科书示例，以演示控制模块的可能用例。
示例 1¶
上面给出了一个未知 **传递函数** 的零极点图。
如果系统的连续时间 **直流增益** 为 **20**，则确定精确的传递函数。
传递函数的性质是 **稳定** 还是 **不稳定**。
获取系统的 **单位脉冲响应**。
在不使用时域方程的情况下，找到系统 **时域响应** 的初始值。
解决方案
>>> # Imports >>> from sympy import symbols, I, limit, pprint, solve, oo >>> from sympy.physics.control import TransferFunction子部分 1
>>> s, k = symbols('s k') >>> gain = k # Let unknwon gain be k >>> a = [-3] # Zero at -3 in S plane >>> b = [-1, -2-I, -2+I] # Poles at -1, (-2, j) and (-2, -j) in S plane >>> tf = TransferFunction.from_zpk(a, b, gain, s) >>> pprint(tf) k*(s + 3) ------------------------------- (s + 1)*(s + 2 - I)*(s + 2 + I) >>> gain = tf.dc_gain() >>> print(gain) 3*k*(2 - I)*(2 + I)/25 >>> K = solve(gain - 20, k)[0] # Solve for k >>> tf = tf.subs({k: K}) # Reconstruct the TransferFunction using .subs() >>> pprint(tf.expand()) 100*s ----- + 100 3 ------------------- 3 2 s + 5*s + 9*s + 5子部分 2
>>> tf.is_stable() # Expect True, since poles lie in the left half of S plane True子部分 3
>>> from sympy import inverse_laplace_transform >>> t = symbols('t', positive = True) >>> # Convert from S to T domain for impulse response >>> tf = tf.to_expr() >>> Impulse_Response = inverse_laplace_transform(tf, s, t) >>> pprint(Impulse_Response) -t -2*t 100*e 100*e *cos(t) ------- - ---------------- 3 3子部分 4
>>> # Apply the Initial Value Theorem on Equation of S domain >>> # limit(y(t), t, 0) = limit(s*Y(S), s, oo) >>> limit(s*tf, s, oo) 0
示例 2¶
找到以下弹簧-质量阻尼系统的传递函数
解决方案
>>> # Imports
>>> from sympy import Function, laplace_transform, laplace_initial_conds, laplace_correspondence, diff, Symbol, solve
>>> from sympy.abc import s, t
>>> from sympy.physics.control import TransferFunction
>>> y = Function('y')
>>> Y = Function('Y')
>>> u = Function('u')
>>> U = Function('U')
>>> k = Symbol('k') # Spring Constant
>>> c = Symbol('c') # Damper
>>> m = Symbol('m') # Mass of block
系统的 **微分方程** 如下所示
\[\begin{split}\frac{{d^2y(t)}}{{dt^2}} + c\frac{{dy(t)}}{{dt}} + ky(t) = w^2u(t) \\\\ 其中初始条件为 \\ y(0) = t,\quad\frac{{dy}}{{dt}}\bigg|_{t=0} = 0\\\end{split}\]>>> f = m*diff(y(t), t, t) + c*diff(y(t), t) + k*y(t) - u(t) >>> F = laplace_transform(f, t, s, noconds=True) >>> F = laplace_correspondence(F, {u: U, y: Y}) >>> F = laplace_initial_conds(F, t, {y: [0, 0]}) >>> t = (solve(F, Y(s))[0])/U(s) # To construct Transfer Function from Y(s) and U(s) >>> tf = TransferFunction.from_rational_expression(t, s) >>> pprint(tf) 1 -------------- 2 c*s + k + m*s
示例 3¶
下面给出了时域中的信号矩阵，也称为 **g(t)** 的 *脉冲响应矩阵*。
\[\begin{split}g(t) = \begin{bmatrix} (1-t)e^{-t} & e^{-2t} \\ -e^{-t}+5e^{-2t} & \left(-3\sqrt{3}\sin\left(\frac{\sqrt{3}t}{2}\right)+\cos\left(\frac{\sqrt{3}t}{2}\right)\right)e^{-\frac{t}{2}} \end{bmatrix}\end{split}\]
关于此矩阵，找到
拉普拉斯域中的系统矩阵（传递函数矩阵）（**g(t)** → **G(s)**）。
系统中输入和输出信号的数量。
系统元素（传递函数矩阵中的各个传递函数）在拉普拉斯域中的 **极点** 和 **零点** *（注意：MIMO 系统的实际极点和零点不是传递函数矩阵中各个元素的极点和零点）*。此外，可视化对应于 **G(s)** 矩阵中 **第一个输入** 和 **第一个输出** 的单个传递函数的极点和零点。
绘制对应于**G(s)**矩阵的**第一个输入**和**第一个输出**的单个传递函数的**单位阶跃响应**。
分析对应于**G(s)**矩阵的**第一个输入**和**第二个输出**的传递函数的Bode幅度和相位图。
解决方案
>>> # Imports >>> from sympy import Matrix, laplace_transform, inverse_laplace_transform, exp, cos, sqrt, sin, pprint >>> from sympy.abc import s, t >>> from sympy.physics.control import *子部分 1
>>> g = Matrix([[exp(-t)*(1 - t), exp(-2*t)], [5*exp((-2*t))-exp((-t)), (cos((sqrt(3)*t)/2) - 3*sqrt(3)*sin((sqrt(3)*t)/2))*exp(-t/2)]]) >>> G = g.applyfunc(lambda a: laplace_transform(a, t, s)[0]) >>> pprint(G) [ 1 1 1 ] [----- - -------- ----- ] [s + 1 2 s + 2 ] [ (s + 1) ] [ ] [ 5 1 s + 1/2 9 ] [ ----- - ----- -------------- - ------------------] [ s + 2 s + 1 2 3 / 2 3\] [ (s + 1/2) + - 2*|(s + 1/2) + -|] [ 4 \ 4/]子部分 2
>>> G = TransferFunctionMatrix.from_Matrix(G, s) >>> type(G) <class 'sympy.physics.control.lti.TransferFunctionMatrix'> >>> type(G[0]) <class 'sympy.physics.control.lti.TransferFunction'> >>> print(f'Inputs = {G.num_inputs}, Outputs = {G.num_outputs}') Inputs = 2, Outputs = 2子部分 3
>>> G.elem_poles() [[[-1, -1, -1], [-2]], [[-2, -1], [-1/2 - sqrt(3)*I/2, -1/2 - sqrt(3)*I/2, -1/2 + sqrt(3)*I/2, -1/2 + sqrt(3)*I/2]]] >>> G.elem_zeros() [[[-1, 0], []], [[-3/4], [4, -1/2 - sqrt(3)*I/2, -1/2 + sqrt(3)*I/2]]] >>> pole_zero_plot(G[0, 0])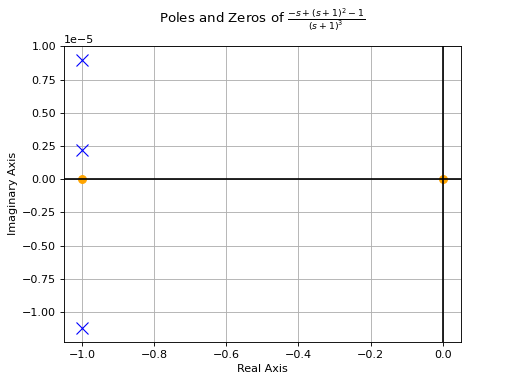
子部分 4
>>> tf1 = G[0, 0] >>> pprint(tf1) 2 -s + (s + 1) - 1 ----------------- 3 (s + 1) >>> step_response_plot(tf1)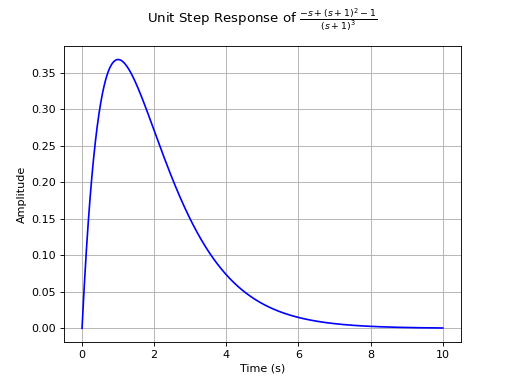
子部分 5
>>> tf2 = G[0, 1] >>> bode_magnitude_plot(tf2)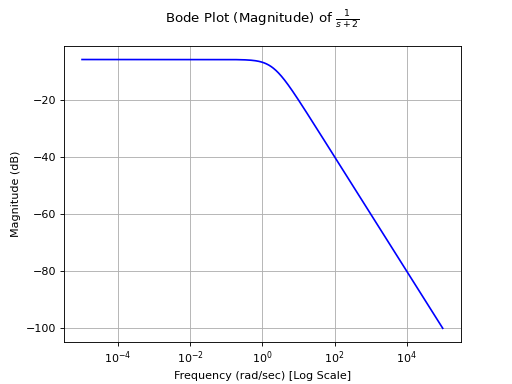
>>> bode_phase_plot(tf2)
示例 4¶
一个系统通过以串联配置排列**P(s)**和**C(s)**来设计（P(s)和C(s)的值在下面给出）。当块的顺序颠倒时（即C(s)然后是P(s)），计算等效系统矩阵。
\[\begin{split}P(s) = \begin{bmatrix} \frac{1}{s} & \frac{2}{s+2} \\ 0 & 3 \end{bmatrix}\end{split}\]\[\begin{split}C(s) = \begin{bmatrix} 1 & 1 \\ 2 & 2 \end{bmatrix}\end{split}\]此外，找到该系统的**等效闭环系统**（或从下面给出的框图中得到的v/u比率）（负反馈回路），该系统具有**C(s)**作为**控制器**和**P(s)**作为**被控对象**（参考下面给出的框图）。
解决方案
>>> # Imports >>> from sympy import Matrix, pprint >>> from sympy.abc import s, t >>> from sympy.physics.control import *子部分 1
>>> P_mat = Matrix([[1/s, 2/(2+s)], [0, 3]]) >>> C_mat = Matrix([[1, 1], [2, 2]]) >>> P = TransferFunctionMatrix.from_Matrix(P_mat, var=s) >>> C = TransferFunctionMatrix.from_Matrix(C_mat, var=s) >>> # Series equivalent, considering (Input)→[P]→[C]→(Output). Note that order of matrix multiplication is opposite to the order in which the elements are arranged. >>> pprint(C*P) [1 1] [1 2 ] [- -] [- -----] [1 1] [s s + 2] [ ] *[ ] [2 2] [0 3 ] [- -] [- - ] [1 1]{t} [1 1 ]{t} >>> # Series equivalent, considering (Input)→[C]→[P]→(Output). >>> pprint(P*C) [1 2 ] [1 1] [- -----] [- -] [s s + 2] [1 1] [ ] *[ ] [0 3 ] [2 2] [- - ] [- -] [1 1 ]{t} [1 1]{t} >>> pprint((C*P).doit()) [1 3*s + 8 ] [- ------- ] [s s + 2 ] [ ] [2 6*s + 16] [- --------] [s s + 2 ]{t} >>> pprint((P*C).doit()) [ 5*s + 2 5*s + 2 ] [--------- ---------] [s*(s + 2) s*(s + 2)] [ ] [ 6 6 ] [ - - ] [ 1 1 ]{t}子部分 2
>>> tfm_feedback = MIMOFeedback(P, C, sign=-1) >>> pprint(tfm_feedback.doit()) # ((I + P*C)**-1)*P [ 7*s + 14 -s - 6 ] [--------------- ---------------] [ 2 2 ] [7*s + 19*s + 2 7*s + 19*s + 2] [ ] [ 2 ] [ -6*s - 12 3*s + 9*s + 6 ] [--------------- ---------------] [ 2 2 ] [7*s + 19*s + 2 7*s + 19*s + 2]{t}
示例 5¶
给定：
\[ \begin{align}\begin{aligned}\begin{split}G1 &= \frac{1}{10 + s}\\\\\end{split}\\\begin{split}G2 &= \frac{1}{1 + s}\\\\\end{split}\\\begin{split}G3 &= \frac{1 + s^2}{4 + 4s + s^2}\\\\\end{split}\\\begin{split}G4 &= \frac{1 + s}{6 + s}\\\\\end{split}\\\begin{split}H1 &= \frac{1 + s}{2 + s}\\\\\end{split}\\\begin{split}H2 &= \frac{2 \cdot (6 + s)}{1 + s}\\\\\end{split}\\\begin{split}H3 &= 1\\\end{split}\end{aligned}\end{align} \]
其中\(s\)是传递函数的变量（在拉普拉斯域）。
求解：
表示上面给定系统的等效传递函数。
系统的零极点图。
解决方案
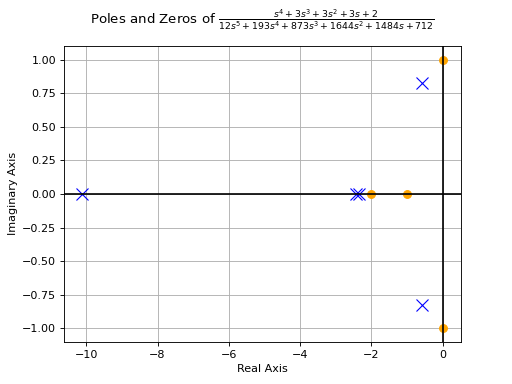
>>> from sympy.abc import s >>> from sympy.physics.control import * >>> G1 = TransferFunction(1, 10 + s, s) >>> G2 = TransferFunction(1, 1 + s, s) >>> G3 = TransferFunction(1 + s**2, 4 + 4*s + s**2, s) >>> G4 = TransferFunction(1 + s, 6 + s, s) >>> H1 = TransferFunction(1 + s, 2 + s, s) >>> H2 = TransferFunction(2*(6 + s), 1 + s, s) >>> H3 = TransferFunction(1, 1, s) >>> sys1 = Series(G3, G4) >>> sys2 = Feedback(sys1, H1, 1).doit() >>> sys3 = Series(G2, sys2) >>> sys4 = Feedback(sys3, H2).doit() >>> sys5 = Series(G1, sys4) >>> sys6 = Feedback(sys5, H3) >>> sys6 # Final unevaluated Feedback object Feedback(Series(TransferFunction(1, s + 10, s), TransferFunction((s + 1)**3*(s + 2)*(s + 6)**2*(s**2 + 1)*(-(s + 1)**2*(s**2 + 1) + (s + 2)*(s + 6)*(s**2 + 4*s + 4))*(s**2 + 4*s + 4)**2, (s + 1)*(s + 6)*(-(s + 1)**2*(s**2 + 1) + (s + 2)*(s + 6)*(s**2 + 4*s + 4))*((s + 1)**2*(s + 6)*(-(s + 1)**2*(s**2 + 1) + (s + 2)*(s + 6)*(s**2 + 4*s + 4))*(s**2 + 4*s + 4) + (s + 1)*(s + 2)*(s + 6)*(2*s + 12)*(s**2 + 1)*(s**2 + 4*s + 4))*(s**2 + 4*s + 4), s)), TransferFunction(1, 1, s), -1) >>> sys6.doit() # Reducing to TransferFunction form without simplification TransferFunction((s + 1)**4*(s + 2)*(s + 6)**3*(s + 10)*(s**2 + 1)*(-(s + 1)**2*(s**2 + 1) + (s + 2)*(s + 6)*(s**2 + 4*s + 4))**2*((s + 1)**2*(s + 6)*(-(s + 1)**2*(s**2 + 1) + (s + 2)*(s + 6)*(s**2 + 4*s + 4))*(s**2 + 4*s + 4) + (s + 1)*(s + 2)*(s + 6)*(2*s + 12)*(s**2 + 1)*(s**2 + 4*s + 4))*(s**2 + 4*s + 4)**3, (s + 1)*(s + 6)*(s + 10)*(-(s + 1)**2*(s**2 + 1) + (s + 2)*(s + 6)*(s**2 + 4*s + 4))*((s + 1)**2*(s + 6)*(-(s + 1)**2*(s**2 + 1) + (s + 2)*(s + 6)*(s**2 + 4*s + 4))*(s**2 + 4*s + 4) + (s + 1)*(s + 2)*(s + 6)*(2*s + 12)*(s**2 + 1)*(s**2 + 4*s + 4))*((s + 1)**3*(s + 2)*(s + 6)**2*(s**2 + 1)*(-(s + 1)**2*(s**2 + 1) + (s + 2)*(s + 6)*(s**2 + 4*s + 4))*(s**2 + 4*s + 4)**2 + (s + 1)*(s + 6)*(s + 10)*(-(s + 1)**2*(s**2 + 1) + (s + 2)*(s + 6)*(s**2 + 4*s + 4))*((s + 1)**2*(s + 6)*(-(s + 1)**2*(s**2 + 1) + (s + 2)*(s + 6)*(s**2 + 4*s + 4))*(s**2 + 4*s + 4) + (s + 1)*(s + 2)*(s + 6)*(2*s + 12)*(s**2 + 1)*(s**2 + 4*s + 4))*(s**2 + 4*s + 4))*(s**2 + 4*s + 4), s) >>> sys6 = sys6.doit(cancel=True, expand=True) # Simplified TransferFunction form >>> sys6 TransferFunction(s**4 + 3*s**3 + 3*s**2 + 3*s + 2, 12*s**5 + 193*s**4 + 873*s**3 + 1644*s**2 + 1484*s + 712, s) >>> pole_zero_plot(sys6)
