生物力学建模介绍¶
sympy.physics.biomechanics 提供功能来增强使用 sympy.physics.mechanics 创建的模型,添加模拟肌肉和肌腱的产生力的元素。在本教程中,我们将介绍该模块的功能。
生物力学包的最初主要目的是引入工具来模拟由 希尔型肌肉模型 产生的力。这些模型基于肌肉的收缩状态和肌腱的被动拉伸,生成施加在生物体骨骼结构上的力。在本教程中,我们将介绍构成肌腱模型的元素,然后演示它在 MusculotendonDeGroote2016 模型中的特定实现。
载荷¶
sympy.physics.mechanics 包含两种类型的载荷:Force 和 Torque。力表示沿作用线方向作用的束缚矢量量,而力矩是无约束矢量,表示一对力产生的力矩。
一个非常常见的力模型的例子是并联的线性弹簧和线性阻尼器。作用在质量为 \(m\) 的粒子上的力,该粒子以广义坐标 \(x(t)\) 描述的 1D 运动,线性弹簧和阻尼系数分别为 \(k\) 和 \(c\),具有熟悉的运动方程
在 SymPy 中,我们可以表述作用在粒子 \(P\) 上的力,该粒子在参考系 \(N\) 中运动,相对于 \(N\) 中固定的点 \(O\) 的位置,如下所示
>>> import sympy as sm
>>> import sympy.physics.mechanics as me
>>> k, c = sm.symbols('k, c', real=True, nonnegative=True)
>>> x = me.dynamicsymbols('x', real=True)
>>> N = me.ReferenceFrame('N')
>>> O, P = me.Point('O'), me.Point('P')
>>> P.set_pos(O, x*N.x)
>>> P.set_vel(N, x.diff()*N.x)
>>> force_on_P = me.Force(P, -k*P.pos_from(O) - c*P.vel(N))
>>> force_on_P
(P, (-c*Derivative(x(t), t) - k*x(t))*N.x)
并且将会有一个大小相等方向相反的力作用在 \(O\) 上
>>> force_on_O = me.Force(O, k*P.pos_from(O) + c*P.vel(N))
>>> force_on_O
(O, (c*Derivative(x(t), t) + k*x(t))*N.x)
单个肌肉和肌腱对一组刚体施加的力将是本教程中进一步开发的肌腱模型的主要输出。
路径¶
肌肉及其相关的肌腱缠绕在移动的骨骼系统以及其他肌肉和器官周围。这带来了确定肌肉和肌腱对骨骼和它接触的器官产生的力的作用线的挑战。我们引入了 pathway 模块来帮助管理对力作用线的几何关系的规范。
上面的弹簧阻尼器示例具有最简单的作用线定义,因此我们可以使用 LinearPathway 来建立这条作用线。首先提供力将有大小相等方向相反作用的两个端点,然后路径通过 length 和 extension_velocity 计算两个点之间的距离和两个点之间的相对速度。请注意,正速度表示两个点彼此远离。还要注意,该公式处理 \(x\) 为正或负的情况。
>>> lpathway = me.LinearPathway(O, P)
>>> lpathway
LinearPathway(O, P)
>>> lpathway.length
Abs(x(t))
>>> lpathway.extension_velocity
sign(x(t))*Derivative(x(t), t)
to_loads 方法然后获取具有符号约定的力的幅值,该符号约定规定正幅值将两个点彼此推开,并返回作用在两个点上的所有力的列表。
>>> import pprint
>>> pprint.pprint(lpathway.to_loads(-k*x - k*x.diff()))
[Force(point=O, force=(k*x(t) + k*Derivative(x(t), t))*x(t)/Abs(x(t))*N.x),
Force(point=P, force=(-k*x(t) - k*Derivative(x(t), t))*x(t)/Abs(x(t))*N.x)]
路径可以用任何任意几何形状和任何数量的相互连接的粒子或刚体构建。例如,更复杂的路径是 ObstacleSetPathway。您可以在两个路径端点之间指定任意数量的中间点,力的驱动路径将沿着这些中间点进行。例如,如果我们在 \(N\) 中引入两个固定点,那么力将沿着连接 \(O\) 到 \(Q\) 到 \(R\) 然后到 \(P\) 的一组线性段作用。所有四个点都会受到力的作用。为简单起见,我们只展示了弹簧力的影响。
>>> Q, R = me.Point('Q'), me.Point('R')
>>> Q.set_pos(O, 1*N.y)
>>> R.set_pos(O, 1*N.x + 1*N.y)
>>> opathway = me.ObstacleSetPathway(O, Q, R, P)
>>> opathway.length
sqrt((x(t) - 1)**2 + 1) + 2
>>> opathway.extension_velocity
(x(t) - 1)*Derivative(x(t), t)/sqrt((x(t) - 1)**2 + 1)
>>> pprint.pprint(opathway.to_loads(-k*opathway.length))
[Force(point=O, force=k*(sqrt((x(t) - 1)**2 + 1) + 2)*N.y),
Force(point=Q, force=- k*(sqrt((x(t) - 1)**2 + 1) + 2)*N.y),
Force(point=Q, force=k*(sqrt((x(t) - 1)**2 + 1) + 2)*N.x),
Force(point=R, force=- k*(sqrt((x(t) - 1)**2 + 1) + 2)*N.x),
Force(point=R, force=k*(sqrt((x(t) - 1)**2 + 1) + 2)*(x(t) - 1)/sqrt((x(t) - 1)**2 + 1)*N.x - k*(sqrt((x(t) - 1)**2 + 1) + 2)/sqrt((x(t) - 1)**2 + 1)*N.y),
Force(point=P, force=- k*(sqrt((x(t) - 1)**2 + 1) + 2)*(x(t) - 1)/sqrt((x(t) - 1)**2 + 1)*N.x + k*(sqrt((x(t) - 1)**2 + 1) + 2)/sqrt((x(t) - 1)**2 + 1)*N.y)]
如果将 \(x=1\) 设置为,更容易看出力的集合是正确的
>>> for load in opathway.to_loads(-k*opathway.length):
... pprint.pprint(me.Force(load[0], load[1].subs({x: 1})))
Force(point=O, force=3*k*N.y)
Force(point=Q, force=- 3*k*N.y)
Force(point=Q, force=3*k*N.x)
Force(point=R, force=- 3*k*N.x)
Force(point=R, force=- 3*k*N.y)
Force(point=P, force=3*k*N.y)
您可以通过子类化 PathwayBase 来创建您自己的路径。
包裹几何形状¶
肌肉在骨骼、组织或器官上包裹很常见。我们引入了包裹几何形状和相关的包裹路径来帮助管理它们的复杂性。例如,如果两个路径端点位于圆柱体的表面上,那么力沿着与连接两个端点处的两个点的测地线的切线作用。该 WrappingCylinder 对象计算路径的复杂几何形状。然后,WrappingPathway 使用该几何形状来构建力。沿着这条路径的弹簧力在下面构建
>>> r = sm.symbols('r', real=True, nonegative=True)
>>> theta = me.dynamicsymbols('theta', real=True)
>>> O, P, Q = sm.symbols('O, P, Q', cls=me.Point)
>>> A = me.ReferenceFrame('A')
>>> A.orient_axis(N, theta, N.z)
>>> P.set_pos(O, r*N.x)
>>> Q.set_pos(O, N.z + r*A.x)
>>> cyl = me.WrappingCylinder(r, O, N.z)
>>> wpathway = me.WrappingPathway(P, Q, cyl)
>>> pprint.pprint(wpathway.to_loads(-k*wpathway.length))
[Force(point=P, force=- k*r*Abs(theta(t))*N.y - k*N.z),
Force(point=Q, force=k*N.z + k*r*Abs(theta(t))*A.y),
Force(point=O, force=k*r*Abs(theta(t))*N.y - k*r*Abs(theta(t))*A.y)]
执行器¶
多体系统模型通常具有以力的幅度或力矩的形式表示的时间变化输入。在许多情况下,这些指定的输入可能来自系统的状态,甚至来自另一个动态系统的输出。该 actuator 模块包括类来帮助管理此类力矩和力输入模型的创建。执行器旨在表示一个真实的物理组件。例如,上面来自弹簧阻尼器的力可以通过子类化 ActuatorBase 并实现一个生成与该弹簧阻尼器执行器相关的载荷的方法来创建。
>>> N = me.ReferenceFrame('N')
>>> O, P = me.Point('O'), me.Point('P')
>>> P.set_pos(O, x*N.x)
>>> class SpringDamper(me.ActuatorBase):
...
... # positive x spring is in tension
... # negative x spring is in compression
... def __init__(self, P1, P2, spring_constant, damper_constant):
... self.P1 = P1
... self.P2 = P2
... self.k = spring_constant
... self.c = damper_constant
...
... def to_loads(self):
... x = self.P2.pos_from(self.P1).magnitude()
... v = x.diff(me.dynamicsymbols._t)
... dir_vec = self.P2.pos_from(self.P1).normalize()
... force_P1 = me.Force(self.P1,
... self.k*x*dir_vec + self.c*v*dir_vec)
... force_P2 = me.Force(self.P2,
... -self.k*x*dir_vec - self.c*v*dir_vec)
... return [force_P1, force_P2]
...
>>> spring_damper = SpringDamper(O, P, k, c)
>>> pprint.pprint(spring_damper.to_loads())
[Force(point=O, force=(c*x(t)*sign(x(t))*Derivative(x(t), t)/Abs(x(t)) + k*x(t))*N.x),
Force(point=P, force=(-c*x(t)*sign(x(t))*Derivative(x(t), t)/Abs(x(t)) - k*x(t))*N.x)]
还有一个 ForceActuator,它允许与路径对象无缝集成。您只需要在子类的初始化中设置 .force 属性。
>>> class SpringDamper(me.ForceActuator):
...
... # positive x spring is in tension
... # negative x spring is in compression
... def __init__(self, pathway, spring_constant, damper_constant):
... self.pathway = pathway
... self.force = (-spring_constant*pathway.length -
... damper_constant*pathway.extension_velocity)
...
>>> spring_damper2 = SpringDamper(lpathway, k, c)
>>> pprint.pprint(spring_damper2.to_loads())
[Force(point=O, force=(c*sign(x(t))*Derivative(x(t), t) + k*Abs(x(t)))*x(t)/Abs(x(t))*N.x),
Force(point=P, force=(-c*sign(x(t))*Derivative(x(t), t) - k*Abs(x(t)))*x(t)/Abs(x(t))*N.x)]
然后,这使得将弹簧阻尼器力应用于其他路径变得容易,例如
>>> spring_damper3 = SpringDamper(wpathway, k, c)
>>> pprint.pprint(spring_damper3.to_loads())
[Force(point=P, force=r*(-c*r**2*theta(t)*Derivative(theta(t), t)/sqrt(r**2*theta(t)**2 + 1) - k*sqrt(r**2*theta(t)**2 + 1))*Abs(theta(t))/sqrt(r**2*theta(t)**2 + 1)*N.y + (-c*r**2*theta(t)*Derivative(theta(t), t)/sqrt(r**2*theta(t)**2 + 1) - k*sqrt(r**2*theta(t)**2 + 1))/sqrt(r**2*theta(t)**2 + 1)*N.z),
Force(point=Q, force=- (-c*r**2*theta(t)*Derivative(theta(t), t)/sqrt(r**2*theta(t)**2 + 1) - k*sqrt(r**2*theta(t)**2 + 1))/sqrt(r**2*theta(t)**2 + 1)*N.z - r*(-c*r**2*theta(t)*Derivative(theta(t), t)/sqrt(r**2*theta(t)**2 + 1) - k*sqrt(r**2*theta(t)**2 + 1))*Abs(theta(t))/sqrt(r**2*theta(t)**2 + 1)*A.y),
Force(point=O, force=- r*(-c*r**2*theta(t)*Derivative(theta(t), t)/sqrt(r**2*theta(t)**2 + 1) - k*sqrt(r**2*theta(t)**2 + 1))*Abs(theta(t))/sqrt(r**2*theta(t)**2 + 1)*N.y + r*(-c*r**2*theta(t)*Derivative(theta(t), t)/sqrt(r**2*theta(t)**2 + 1) - k*sqrt(r**2*theta(t)**2 + 1))*Abs(theta(t))/sqrt(r**2*theta(t)**2 + 1)*A.y)]
激活动力学¶
肌腱模型能够在激活时产生主动收缩力。从生物学角度看,当 \(\textrm{Ca}^{2+}\) 离子以足够的浓度存在于肌肉纤维中时,它们会开始自愿收缩。这种自愿收缩状态称为“激活”。在生物力学模型中,它通常用符号 \(a(t)\) 表示,该符号被视为在范围 \([0, 1]\) 内的归一化量。
生物体不直接控制其肌肉中这些 \(\textrm{Ca}^{2+}\) 离子的浓度,而是由其大脑控制的神经系统向肌肉发送电信号,导致 \(\textrm{Ca}^{2+}\) 离子释放。这些离子扩散并增加在整个肌肉中的浓度,从而导致激活。传输到刺激收缩的肌肉的电信号称为“兴奋”。在生物力学模型中,它通常用符号 \(e(t)\) 表示,该符号也被视为在范围 \([0, 1]\) 内的归一化量。
兴奋输入和激活状态之间的关系称为激活动力学。由于激活动力学在生物力学模型中非常普遍,SymPy 提供了 activation 模块,其中包含一些常见激活动力学模型的实现。这些是基于 [DeGroote2016] 论文中的方程的零阶激活动力学和一阶激活动力学。下面,我们将逐步完成手动实现这些模型的过程,然后展示它们如何与 SymPy 提供的类相关。
零阶¶
激活动力学的最简单模型是假设 \(\textrm{Ca}^{2+}\) 离子的扩散是瞬时的。在数学上,这给了我们 \(a(t) = e(t)\),一个零阶常微分方程。
>>> e = me.dynamicsymbols('e')
>>> e
e(t)
>>> a = e
>>> a
e(t)
或者,您可以让 \(a(t)\) 有自己的 dynamicsymbols,并在任何方程中使用替换将此替换为 \(e(t)\)。
>>> a = me.dynamicsymbols('a')
>>> zeroth_order_activation = {a: e}
>>> a.subs(zeroth_order_activation)
e(t)
SymPy 在 activation 模块中提供了类 ZerothOrderActivation。必须使用单个参数 name 实例化此类,该参数将名称与实例关联。此名称在每个实例中都应该是唯一的。
>>> from sympy.physics.biomechanics import ZerothOrderActivation
>>> actz = ZerothOrderActivation('zeroth')
>>> actz
ZerothOrderActivation('zeroth')
传递给 \(name\) 的参数试图帮助确保为 \(e(t)\) 和 \(a(t)\) 自动创建的 dynamicsymbols 在实例之间是唯一的。
>>> actz.excitation
e_zeroth(t)
>>> actz.activation
e_zeroth(t)
ZerothOrderActivation 是 ActivationBase 的子类,它为所有具体的激活动力学类提供了统一的接口。这包括检查与模型相关的常微分方程(组)的方法。由于零阶激活动力学对应于零阶常微分方程,因此它返回一个空列矩阵。
>>> actz.rhs()
Matrix(0, 1, [])
一阶¶
在实际情况中,\(\textrm{Ca}^{2+}\)离子的扩散和浓度增加并非瞬时完成的。在真实的生物肌肉中,兴奋的阶跃增加会导致激活平滑且逐渐增加。 [DeGroote2016] 使用一阶常微分方程来模拟这种情况。
其中 \(\tau_a\) 是激活时间常数,\(\tau_d\) 是失活时间常数,\(b\) 是平滑系数。
>>> tau_a, tau_d, b = sm.symbols('tau_a, tau_d, b')
>>> f = sm.tanh(b*(e - a))/2
>>> dadt = ((1/(tau_a*(1 + 3*a)))*(1 + 2*f) + ((1 + 3*a)/(4*tau_d))*(1 - 2*f))*(e - a)
这个一阶常微分方程可以用来在模拟中传播状态 \(a(t)\),输入为 \(e(t)\)。
和之前一样,SymPy 在 activation 模块中提供了名为 FirstOrderActivationDeGroote2016 的类。这个类是 ActivationBase 的另一个子类,并使用上述 [DeGroote2016] 中定义的一阶激活动力学模型。这个类必须使用四个参数进行实例化:一个名称,以及三个可符号化的对象,用于表示三个常数 \(\tau_a\),\(\tau_d\) 和 \(b\)。
>>> from sympy.physics.biomechanics import FirstOrderActivationDeGroote2016
>>> actf = FirstOrderActivationDeGroote2016('first', tau_a, tau_d, b)
>>> actf.excitation
e_first(t)
>>> actf.activation
a_first(t)
和之前一样,可以通过访问一阶常微分方程,但这次返回的是一个长度为 1 的列向量。
>>> actf.rhs()
Matrix([[((1/2 - tanh(b*(-a_first(t) + e_first(t)))/2)*(3*a_first(t)/2 + 1/2)/tau_d + (tanh(b*(-a_first(t) + e_first(t)))/2 + 1/2)/(tau_a*(3*a_first(t)/2 + 1/2)))*(-a_first(t) + e_first(t))]])
你也可以使用每个常数的建议值来实例化该类。这些值是:\(\tau_a = 0.015\),\(\tau_d = 0.060\),以及 \(b = 10.0\)。
>>> actf2 = FirstOrderActivationDeGroote2016.with_defaults('first')
>>> actf2.rhs()
Matrix([[((1/2 - tanh(10.0*a_first(t) - 10.0*e_first(t))/2)/(0.0225*a_first(t) + 0.0075) + 16.6666666666667*(3*a_first(t)/2 + 1/2)*(tanh(10.0*a_first(t) - 10.0*e_first(t))/2 + 1/2))*(-a_first(t) + e_first(t))]])
>>> constants = {tau_a: sm.Float('0.015'), tau_d: sm.Float('0.060'), b: sm.Float('10.0')}
>>> actf.rhs().subs(constants)
Matrix([[(66.6666666666667*(1/2 - tanh(10.0*a_first(t) - 10.0*e_first(t))/2)/(3*a_first(t)/2 + 1/2) + 16.6666666666667*(3*a_first(t)/2 + 1/2)*(tanh(10.0*a_first(t) - 10.0*e_first(t))/2 + 1/2))*(-a_first(t) + e_first(t))]])
自定义¶
要创建自己的激活动力学自定义模型,你可以继承 ActivationBase 并覆盖抽象方法。然后,具体类将符合预期的 API,并自动与 sympy.physics.mechanics 和 sympy.physics.biomechanics 中的其他部分集成。
肌腱曲线¶
多年来,已经发表了许多不同配置的 Hill 型肌肉模型,这些模型包含了不同组合的串联和并联元件。我们将考虑一个非常常见的模型版本,该模型将肌腱建模为与肌肉纤维串联的元件,而肌肉纤维又被建模为三个并联元件:弹性元件、收缩元件和阻尼器。
显示四元件 Hill 型肌肉模型的示意图。 \(SE\) 是代表肌腱的串联元件,\(CE\) 是收缩元件,\(EE\) 是代表肌肉纤维弹性的并联元件,\(DE\) 是阻尼器。¶
这些组件中的每一个通常都有一个描述它的特征曲线。以下小节将描述和实现 [DeGroote2016] 论文中描述的特征曲线。
肌腱力-长度¶
通常将肌腱建模为刚性(不可伸展)和弹性元件。如果肌腱被视为刚性,则肌腱长度不会发生变化,肌肉纤维的长度会随着肌腱长度的变化而直接变化。刚性肌腱不会有相关的特征曲线;它本身没有产生力的能力,只是直接传递肌肉纤维产生的力。
如果肌腱是弹性的,它通常被建模为非线性弹簧。因此,我们有了第一个特征曲线,即肌腱力-长度曲线,它是归一化肌腱长度的函数
其中 \(l^T\) 是肌腱长度,\(l^T_{slack}\) 是“肌腱松弛长度”,一个代表肌腱在无力状态下的长度的常数。特征性肌腱曲线是根据“归一化”(或“无量纲”)量(如 \(\tilde{l}^T\))来参数化的,因为这些曲线普遍适用于所有肌肉纤维和肌腱。可以通过选择不同常数值来调整它们的属性以模拟特定的肌腱。在肌腱力-长度特征的情况下,这是通过调整 \(l^T_{slack}\) 来实现的。该常数的值越短,肌腱越硬。
来自 [DeGroote2016] 的肌腱力-长度曲线的方程 \(fl^T\left(\tilde{l}^T\right)\) 为
为了在 SymPy 中实现这一点,我们需要一个代表 \(\tilde{l}^T\) 的随时间变化的动态符号,以及四个代表四个常数的符号。
>>> l_T_tilde = me.dynamicsymbols('l_T_tilde')
>>> c0, c1, c2, c3 = sm.symbols('c0, c1, c2, c3')
>>> fl_T = c0*sm.exp(c3*(l_T_tilde - c1)) - c2
>>> fl_T
c0*exp(c3*(-c1 + l_T_tilde(t))) - c2
或者,我们可以根据 \(l^T\) 和 \(l^T_{slack}\) 来定义它。
>>> l_T = me.dynamicsymbols('l_T')
>>> l_T_slack = sm.symbols('l_T_slack')
>>> fl_T = c0*sm.exp(c3*(l_T/l_T_slack - c1)) - c2
>>> fl_T
c0*exp(c3*(-c1 + l_T(t)/l_T_slack)) - c2
SymPy 中的 biomechanics 模块为此曲线提供了一个类,名为 TendonForceLengthDeGroote2016。它可以使用五个参数进行实例化。第一个参数是 \(\tilde{l}^T\),它不一定是符号;它可以是一个表达式。另外四个参数都是常数。目的是让这些参数成为常数,或者可符号化的数值。
>>> from sympy.physics.biomechanics import TendonForceLengthDeGroote2016
>>> fl_T2 = TendonForceLengthDeGroote2016(l_T/l_T_slack, c0, c1, c2, c3)
>>> fl_T2
TendonForceLengthDeGroote2016(l_T(t)/l_T_slack, c0, c1, c2, c3)
这个类是 Function 的子类,因此它实现了 SymPy 的常用方法,用于替换、评估、微分等。 doit 方法允许访问曲线的方程。
>>> fl_T2.doit()
c0*exp(c3*(-c1 + l_T(t)/l_T_slack)) - c2
该类提供了一个备用构造函数,允许它使用 [DeGroote2016] 中推荐的常数值进行预填充构造。这需要一个参数,也对应于 \(\tilde{l}^T\),它可以是符号或表达式。
>>> fl_T3 = TendonForceLengthDeGroote2016.with_defaults(l_T/l_T_slack)
>>> fl_T3
TendonForceLengthDeGroote2016(l_T(t)/l_T_slack, 0.2, 0.995, 0.25, 33.93669377311689)
在上面的代码中,常数已经被 SymPy 数值类型的实例(如 Float)所替换。
TendonForceLengthDeGroote2016 类还支持代码生成,因此可以与 SymPy 的代码打印器无缝集成。为了可视化这条曲线,我们可以使用 lambdify 来实例化该函数,它将创建一个可调用函数,用于评估给定 \(\tilde{l}^T\) 值的函数。 \(\tilde{l}^T\) 的合理值位于 \([0.95, 1.05]\) 范围内,我们将在下面对其进行绘图。
>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from sympy.physics.biomechanics import TendonForceLengthDeGroote2016
>>> l_T_tilde = me.dynamicsymbols('l_T_tilde')
>>> fl_T = TendonForceLengthDeGroote2016.with_defaults(l_T_tilde)
>>> fl_T_callable = sm.lambdify(l_T_tilde, fl_T)
>>> l_T_tilde_num = np.linspace(0.95, 1.05)
>>> fig, ax = plt.subplots()
>>> _ = ax.plot(l_T_tilde_num, fl_T_callable(l_T_tilde_num))
>>> _ = ax.set_xlabel('Normalized tendon length')
>>> _ = ax.set_ylabel('Normalized tendon force-length')
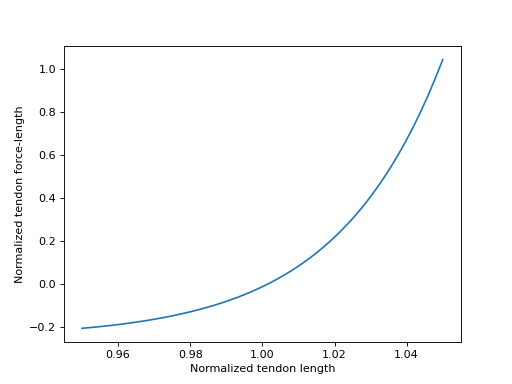
在推导具有弹性肌腱的模型的肌腱动力学方程时,了解肌腱力-长度特征曲线的反函数可能会有用。 [DeGroote2016] 中定义的曲线在分析上是可逆的,这意味着我们可以直接确定 \(\tilde{l}^T = \left[fl^T\left(\tilde{l}^T\right)\right]^{-1}\),对于给定的 \(fl^T\left(\tilde{l}^T\right)\) 值。
biomechanics 中也存在一个类,名为 TendonForceLengthInverseDeGroote2016,它的行为与 TendonForceLengthDeGroote2016 相同。它可以使用五个参数进行实例化,第一个参数是 \(fl^T\),后面跟着四个常数,或者使用备用构造函数,使用单个参数来表示 \(fl^T\)。
>>> from sympy.physics.biomechanics import TendonForceLengthInverseDeGroote2016
>>> fl_T_sym =me.dynamicsymbols('fl_T')
>>> fl_T_inv = TendonForceLengthInverseDeGroote2016(fl_T_sym, c0, c1, c2, c3)
>>> fl_T_inv
TendonForceLengthInverseDeGroote2016(fl_T(t), c0, c1, c2, c3)
>>> fl_T_inv2 = TendonForceLengthInverseDeGroote2016.with_defaults(fl_T_sym)
>>> fl_T_inv2
TendonForceLengthInverseDeGroote2016(fl_T(t), 0.2, 0.995, 0.25, 33.93669377311689)
纤维被动力-长度¶
用于模拟肌肉纤维的第一个元件是纤维被动力-长度。这本质上是另一个代表肌肉纤维弹性特性的非线性弹簧。描述该元件的特征曲线是归一化肌肉纤维长度的函数
其中 \(l^M\) 是肌肉纤维长度,而 \(l^M_{opt}\) 是“最佳纤维长度”,一个常数,表示肌肉纤维在该长度下不产生被动弹性力(这也是肌肉纤维能够产生最大主动力的长度)。类似于调整 \(l^T_{slack}\) 来改变通过肌腱力-长度特性建模的肌腱的刚度特性,我们可以调整 \(l^M_{opt}\) 来改变肌肉纤维的被动特性;减小 \(l^M_{opt}\) 将使建模的肌肉纤维更硬。
纤维被动力-长度曲线的方程 \(fl^M_{pas}\left(\tilde{l}^M\right)\) 来自 [DeGroote2016] 是
与之前类似,为了在 SymPy 中实现这一点,我们需要一个代表 \(\tilde{l}^M\) 的随时间变化的动态符号和两个代表两个常数的符号。
>>> l_M_tilde = me.dynamicsymbols('l_M_tilde')
>>> c0, c1 = sm.symbols('c0, c1')
>>> fl_M_pas = (sm.exp(c1*(l_M_tilde - 1)/c0) - 1)/(sm.exp(c1) - 1)
>>> fl_M_pas
(exp(c1*(l_M_tilde(t) - 1)/c0) - 1)/(exp(c1) - 1)
或者,我们可以用 \(l^M\) 和 \(l^M_{opt}\) 来定义。
>>> l_M = me.dynamicsymbols('l_M')
>>> l_M_opt = sm.symbols('l_M_opt')
>>> fl_M_pas2 = (sm.exp(c1*(l_M/l_M_opt - 1)/c0) - 1)/(sm.exp(c1) - 1)
>>> fl_M_pas2
(exp(c1*(-1 + l_M(t)/l_M_opt)/c0) - 1)/(exp(c1) - 1)
同样,SymPy 中的 biomechanics 模块为此曲线提供了一个类,FiberForceLengthPassiveDeGroote2016。它可以用三个参数实例化。第一个参数是 \(\tilde{l}^M\),它不一定是符号,可以是表达式。后面的两个参数都是常数。它们被设计为常数,或可简化的数值。
>>> from sympy.physics.biomechanics import FiberForceLengthPassiveDeGroote2016
>>> fl_M_pas2 = FiberForceLengthPassiveDeGroote2016(l_M/l_M_opt, c0, c1)
>>> fl_M_pas2
FiberForceLengthPassiveDeGroote2016(l_M(t)/l_M_opt, c0, c1)
>>> fl_M_pas2.doit()
(exp(c1*(-1 + l_M(t)/l_M_opt)/c0) - 1)/(exp(c1) - 1)
使用备用构造函数,它为 \(\tilde{l}^M\) 接受单个参数,我们可以创建一个预先填充了 [DeGroote2016] 中推荐的常数值的实例。
>>> fl_M_pas3 = FiberForceLengthPassiveDeGroote2016.with_defaults(l_M/l_M_opt)
>>> fl_M_pas3
FiberForceLengthPassiveDeGroote2016(l_M(t)/l_M_opt, 0.6, 4.0)
>>> fl_M_pas3.doit()
2.37439874427164e-5*exp(6.66666666666667*l_M(t)/l_M_opt) - 0.0186573603637741
\(\tilde{l}^M\) 的合理值在 \([0.0, 2.0]\) 范围内,我们将在下面绘制该范围内的曲线。
>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from sympy.physics.biomechanics import FiberForceLengthPassiveDeGroote2016
>>> l_M_tilde = me.dynamicsymbols('l_M_tilde')
>>> fl_M_pas = FiberForceLengthPassiveDeGroote2016.with_defaults(l_M_tilde)
>>> fl_M_pas_callable = sm.lambdify(l_M_tilde, fl_M_pas)
>>> l_M_tilde_num = np.linspace(0.0, 2.0)
>>> fig, ax = plt.subplots()
>>> _ = ax.plot(l_M_tilde_num, fl_M_pas_callable(l_M_tilde_num))
>>> _ = ax.set_xlabel('Normalized fiber length')
>>> _ = ax.set_ylabel('Normalized fiber passive force-length')
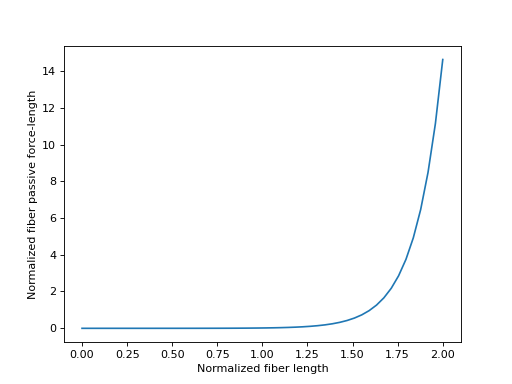
在制定肌腱动力学时,有时需要纤维被动力-长度特性曲线的反函数。来自 [DeGroote2016] 的这条曲线的方程再次是可解析反转的。
在 biomechanics 中也有一个为此函数提供的类,FiberForceLengthPassiveInverseDeGroote2016。它可以用三个参数实例化,第一个参数是 \(fl^M\),后面跟着一对常数,或者使用备用构造函数,它接受 \(\tilde{l}^M\) 的单个参数。
>>> from sympy.physics.biomechanics import FiberForceLengthPassiveInverseDeGroote2016
>>> fl_M_pas_sym =me.dynamicsymbols('fl_M_pas')
>>> fl_M_pas_inv = FiberForceLengthPassiveInverseDeGroote2016(fl_M_pas_sym, c0, c1)
>>> fl_M_pas_inv
FiberForceLengthPassiveInverseDeGroote2016(fl_M_pas(t), c0, c1)
>>> fl_M_pas_inv2 = FiberForceLengthPassiveInverseDeGroote2016.with_defaults(fl_M_pas_sym)
>>> fl_M_pas_inv2
FiberForceLengthPassiveInverseDeGroote2016(fl_M_pas(t), 0.6, 4.0)
纤维主动力-长度¶
当肌肉被激活时,它收缩以产生力量。这种现象由肌腱模型中平行纤维成分中的收缩元件建模。纤维能够产生的力量大小是纤维瞬时长度的函数。描述纤维主动力-长度曲线的特征曲线再次由 \(\tilde{l}^M\) 参数化。这条曲线是“钟形”的。对于 \(\tilde{l}^M\) 的非常小和非常大的值,主动纤维力-长度趋于零。峰值主动纤维力-长度发生在 \(\tilde{l}^M = l^M_{opt}\) 处,值为 \(0.0\)。
纤维主动力-长度曲线的方程 \(fl^M_{act}\left(\tilde{l}^M\right)\) 来自 [DeGroote2016] 是
为了在 SymPy 中实现这一点,我们需要一个代表 \(\tilde{l}^M\) 的随时间变化的动态符号和十二个代表十二个常数的符号。
>>> constants = sm.symbols('c0:12')
>>> c0, c1, c2, c3, c4, c5, c6, c7, c8, c9, c10, c11 = constants
>>> fl_M_act = (c0*sm.exp(-(((l_M_tilde - c1)/(c2 + c3*l_M_tilde))**2)/2) + c4*sm.exp(-(((l_M_tilde - c5)/(c6 + c7*l_M_tilde))**2)/2) + c8*sm.exp(-(((l_M_tilde - c9)/(c10 + c11*l_M_tilde))**2)/2))
>>> fl_M_act
c0*exp(-(-c1 + l_M_tilde(t))**2/(2*(c2 + c3*l_M_tilde(t))**2)) + c4*exp(-(-c5 + l_M_tilde(t))**2/(2*(c6 + c7*l_M_tilde(t))**2)) + c8*exp(-(-c9 + l_M_tilde(t))**2/(2*(c10 + c11*l_M_tilde(t))**2))
SymPy 为此曲线提供的类是 FiberForceLengthActiveDeGroote2016。它可以用十三个参数实例化。第一个参数是 \(\tilde{l}^M\),它不一定是符号,可以是表达式。后面的十二个参数都是常数。它们被设计为常数,或可简化的数值。
>>> from sympy.physics.biomechanics import FiberForceLengthActiveDeGroote2016
>>> fl_M_act2 = FiberForceLengthActiveDeGroote2016(l_M/l_M_opt, *constants)
>>> fl_M_act2
FiberForceLengthActiveDeGroote2016(l_M(t)/l_M_opt, c0, c1, c2, c3, c4, c5, c6, c7, c8, c9, c10, c11)
>>> fl_M_act2.doit()
c0*exp(-(-c1 + l_M(t)/l_M_opt)**2/(2*(c2 + c3*l_M(t)/l_M_opt)**2)) + c4*exp(-(-c5 + l_M(t)/l_M_opt)**2/(2*(c6 + c7*l_M(t)/l_M_opt)**2)) + c8*exp(-(-c9 + l_M(t)/l_M_opt)**2/(2*(c10 + c11*l_M(t)/l_M_opt)**2))
使用备用构造函数,它为 \(\tilde{l}^M\) 接受单个参数,我们可以创建一个预先填充了 [DeGroote2016] 中推荐的常数值的实例。
>>> fl_M_act3 = FiberForceLengthActiveDeGroote2016.with_defaults(l_M/l_M_opt)
>>> fl_M_act3
FiberForceLengthActiveDeGroote2016(l_M(t)/l_M_opt, 0.814, 1.06, 0.162, 0.0633, 0.433, 0.717, -0.0299, 0.2, 0.1, 1.0, 0.354, 0.0)
>>> fl_M_act3.doit()
0.1*exp(-3.98991349867535*(-1 + l_M(t)/l_M_opt)**2) + 0.433*exp(-12.5*(-0.717 + l_M(t)/l_M_opt)**2/(-0.1495 + l_M(t)/l_M_opt)**2) + 0.814*exp(-21.4067977442463*(-1 + 0.943396226415094*l_M(t)/l_M_opt)**2/(1 + 0.390740740740741*l_M(t)/l_M_opt)**2)
\(\tilde{l}^M\) 的合理值在 \([0.0, 2.0]\) 范围内,我们将在下面绘制该范围内的曲线。
>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from sympy.physics.biomechanics import FiberForceLengthActiveDeGroote2016
>>> l_M_tilde = me.dynamicsymbols('l_M_tilde')
>>> fl_M_act = FiberForceLengthActiveDeGroote2016.with_defaults(l_M_tilde)
>>> fl_M_act_callable = sm.lambdify(l_M_tilde, fl_M_act)
>>> l_M_tilde_num = np.linspace(0.0, 2.0)
>>> fig, ax = plt.subplots()
>>> _ = ax.plot(l_M_tilde_num, fl_M_act_callable(l_M_tilde_num))
>>> _ = ax.set_xlabel('Normalized fiber length')
>>> _ = ax.set_ylabel('Normalized fiber active force-length')
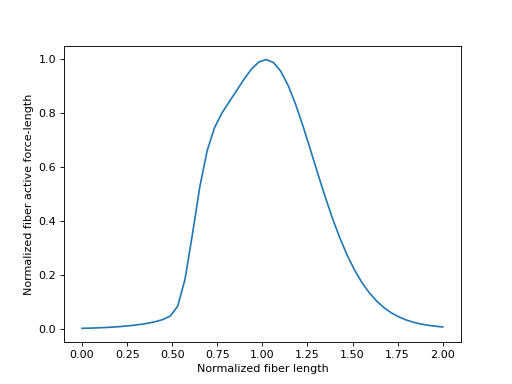
对于纤维主动力-长度特性曲线,不存在反函数,因为它在每个 \(fl^M_{act}\) 值下有多个 \(\tilde{l}^M\) 值。
纤维力-速度¶
收缩元件产生的力量也是其伸长速度的函数。描述收缩元件动力学中与速度相关的部分的特征曲线是归一化肌肉纤维伸长速度的函数
其中 \(v^M\) 是肌肉纤维伸长速度,而 \(v^M_{max}\) 是“最大纤维速度”,一个常数,表示肌肉纤维在该速度下在同心收缩时无法产生任何收缩力。 \(v^M_{max}\) 通常取值为 \(10 l^M_{opt}\)。
纤维力-速度曲线的方程 \(fv^M\left(\tilde{v}^M\right)\) 来自 [DeGroote2016] 是
与之前类似,为了在 SymPy 中实现这一点,我们需要一个代表 \(\tilde{v}^M\) 的随时间变化的动态符号和四个代表四个常数的符号。
>>> v_M_tilde = me.dynamicsymbols('v_M_tilde')
>>> c0, c1, c2, c3 = sm.symbols('c0, c1, c2, c3')
>>> fv_M = c0*sm.log(c1*v_M_tilde + c2 + sm.sqrt((c1*v_M_tilde + c2)**2 + 1)) + c3
>>> fv_M
c0*log(c1*v_M_tilde(t) + c2 + sqrt((c1*v_M_tilde(t) + c2)**2 + 1)) + c3
或者,我们可以用 \(v^M\) 和 \(v^M_{max}\) 来定义。
>>> v_M = me.dynamicsymbols('v_M')
>>> v_M_max = sm.symbols('v_M_max')
>>> fv_M_pas2 = c0*sm.log(c1*v_M/v_M_max + c2 + sm.sqrt((c1*v_M/v_M_max + c2)**2 + 1)) + c3
>>> fv_M_pas2
c0*log(c1*v_M(t)/v_M_max + c2 + sqrt((c1*v_M(t)/v_M_max + c2)**2 + 1)) + c3
SymPy 为此曲线提供的类是 FiberForceVelocityDeGroote2016。它可以用五个参数实例化。第一个参数是 \(\tilde{v}^M\),它不一定是符号,可以是表达式。后面的四个参数都是常数。它们被设计为常数,或可简化的数值。
>>> from sympy.physics.biomechanics import FiberForceVelocityDeGroote2016
>>> fv_M2 = FiberForceVelocityDeGroote2016(v_M/v_M_max, c0, c1, c2, c3)
>>> fv_M2
FiberForceVelocityDeGroote2016(v_M(t)/v_M_max, c0, c1, c2, c3)
>>> fv_M2.doit()
c0*log(c1*v_M(t)/v_M_max + c2 + sqrt((c1*v_M(t)/v_M_max + c2)**2 + 1)) + c3
使用备用构造函数,它为 \(\tilde{v}^M\) 接受单个参数,我们可以创建一个预先填充了 [DeGroote2016] 中推荐的常数值的实例。
>>> fv_M3 = FiberForceVelocityDeGroote2016.with_defaults(v_M/v_M_max)
>>> fv_M3
FiberForceVelocityDeGroote2016(v_M(t)/v_M_max, -0.318, -8.149, -0.374, 0.886)
>>> fv_M3.doit()
0.886 - 0.318*log(8.149*sqrt((-0.0458952018652595 - v_M(t)/v_M_max)**2 + 0.0150588346410601) - 0.374 - 8.149*v_M(t)/v_M_max)
\(\tilde{v}^M\) 的合理值在 \([-1.0, 1.0]\) 范围内,我们将在下面绘制该范围内的曲线。
>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from sympy.physics.biomechanics import FiberForceVelocityDeGroote2016
>>> v_M_tilde = me.dynamicsymbols('v_M_tilde')
>>> fv_M = FiberForceVelocityDeGroote2016.with_defaults(v_M_tilde)
>>> fv_M_callable = sm.lambdify(v_M_tilde, fv_M)
>>> v_M_tilde_num = np.linspace(-1.0, 1.0)
>>> fig, ax = plt.subplots()
>>> _ = ax.plot(l_M_tilde_num, fv_M_callable(v_M_tilde_num))
>>> _ = ax.set_xlabel('Normalized fiber velocity')
>>> _ = ax.set_ylabel('Normalized fiber force-velocity')
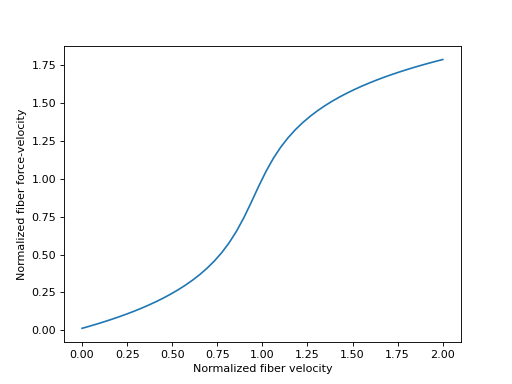
在制定肌腱动力学时,有时需要纤维力-速度特性曲线的反函数。来自 [DeGroote2016] 的这条曲线的方程再次是可解析反转的。
在 biomechanics 中也有一个为此函数提供的类,FiberForceVelocityInverseDeGroote2016。它可以用五个参数实例化,第一个参数是 \(fv^M\),后面跟着四个常数,或者使用备用构造函数,它接受 \(\tilde{v}^M\) 的单个参数。
>>> from sympy.physics.biomechanics import FiberForceVelocityInverseDeGroote2016
>>> fv_M_sym = me.dynamicsymbols('fv_M')
>>> fv_M_inv = FiberForceVelocityInverseDeGroote2016(fv_M_sym, c0, c1, c2, c3)
>>> fv_M_inv
FiberForceVelocityInverseDeGroote2016(fv_M(t), c0, c1, c2, c3)
>>> fv_M_inv2 = FiberForceVelocityInverseDeGroote2016.with_defaults(fv_M_sym)
>>> fv_M_inv2
FiberForceVelocityInverseDeGroote2016(fv_M(t), -0.318, -8.149, -0.374, 0.886)
纤维阻尼¶
肌腱模型中最简单的元素可能是纤维阻尼。它没有相关的特征曲线,因为它通常被建模为一个简单的线性阻尼器。我们将使用 \(\beta\) 作为阻尼系数,使得阻尼力可以描述为
[DeGroote2016] 建议使用 \(\beta = 0.1\) 的值。但是,SymPy 默认使用 \(\beta = 10\)。在进行正向模拟或求解最优控制问题时,这种阻尼的增加通常不会显著影响肌腱动力学,但已被实证发现显著提高了方程的数值条件。
肌腱动力学¶
刚性肌腱动力学¶
刚性肌腱肌腱动力学相对容易实现,因为不可伸长的肌腱允许用肌腱长度直接表示归一化肌肉纤维长度。对于不可伸长的肌腱 \(l^T = l^T_{slack}\),因此归一化肌腱长度只是 1,\(\tilde{l}^T = 1\)。使用三角学,肌肉纤维长度可以表示为
其中 \(\alpha_{opt}\) 是“最佳羽化角”,另一个肌腱的常数属性,描述了羽化角(肌肉纤维相对于平行于肌腱的方向的角度),在该角度下 \(l^M = l^M_{opt}\)。一个常见的简化假设是假设 \(\alpha_{opt} = 0\),这将上述公式简化为
用 \(\tilde{l}^M = \frac{l^M}{l^M_{opt}}\),肌肉纤维速度可以表示为
肌肉纤维可以像以前一样归一化,\(\tilde{v}^M = \frac{v^M}{v^M_{max}}\)。使用上面描述的曲线,我们可以将归一化的肌肉纤维力 (\(\tilde{F}^M\)) 表示为归一化的肌腱长度 (\(\tilde{l}^T\))、归一化的纤维长度 (\(\tilde{l}^M\))、归一化的纤维速度 (\(\tilde{v}^M\)) 和激活 (\(a\)) 的函数
我们引入一个新的常数 \(F^M_{max}\),即“最大等长力”,它描述了肌腱在完全激活和等长 (\(v^M = 0\)) 收缩下所能产生的最大力。考虑到羽化角,肌腱力 (\(F^T\)),即施加到骨骼上肌腱的起点和插入点的力,可以表示为
我们可以使用 SymPy 和我们上面介绍的肌腱曲线类来描述所有这些。我们需要 \(l^{MT}\)、\(v_{MT}\) 和 \(a\) 的时变动力学符号。我们还需要 \(l^T_{slack}\)、\(l^M_{opt}\)、\(F^M_{max}\)、\(v^M_{max}\)、\(\alpha_{opt}\) 和 \(\beta\) 的常数符号。
>>> l_MT, v_MT, a = me.dynamicsymbols('l_MT, v_MT, a')
>>> l_T_slack, l_M_opt, F_M_max = sm.symbols('l_T_slack, l_M_opt, F_M_max')
>>> v_M_max, alpha_opt, beta = sm.symbols('v_M_max, alpha_opt, beta')
>>> l_M = sm.sqrt((l_MT - l_T_slack)**2 + (l_M_opt*sm.sin(alpha_opt))**2)
>>> l_M
sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)
>>> v_M = v_MT*(l_MT - l_T_slack)/l_M
>>> v_M
(-l_T_slack + l_MT(t))*v_MT(t)/sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)
>>> fl_M_pas = FiberForceLengthPassiveDeGroote2016.with_defaults(l_M/l_M_opt)
>>> fl_M_pas
FiberForceLengthPassiveDeGroote2016(sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)/l_M_opt, 0.6, 4.0)
>>> fl_M_act = FiberForceLengthActiveDeGroote2016.with_defaults(l_M/l_M_opt)
>>> fl_M_act
FiberForceLengthActiveDeGroote2016(sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)/l_M_opt, 0.814, 1.06, 0.162, 0.0633, 0.433, 0.717, -0.0299, 0.2, 0.1, 1.0, 0.354, 0.0)
>>> fv_M = FiberForceVelocityDeGroote2016.with_defaults(v_M/v_M_max)
>>> fv_M
FiberForceVelocityDeGroote2016((-l_T_slack + l_MT(t))*v_MT(t)/(v_M_max*sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)), -0.318, -8.149, -0.374, 0.886)
>>> F_M = a*fl_M_act*fv_M + fl_M_pas + beta*v_M/v_M_max
>>> F_M
beta*(-l_T_slack + l_MT(t))*v_MT(t)/(v_M_max*sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)) + a(t)*FiberForceLengthActiveDeGroote2016(sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)/l_M_opt, 0.814, 1.06, 0.162, 0.0633, 0.433, 0.717, -0.0299, 0.2, 0.1, 1.0, 0.354, 0.0)*FiberForceVelocityDeGroote2016((-l_T_slack + l_MT(t))*v_MT(t)/(v_M_max*sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)), -0.318, -8.149, -0.374, 0.886) + FiberForceLengthPassiveDeGroote2016(sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)/l_M_opt, 0.6, 4.0)
>>> F_T = F_M_max*F_M*sm.sqrt(1 - sm.sin(alpha_opt)**2)
>>> F_T
F_M_max*sqrt(1 - sin(alpha_opt)**2)*(beta*(-l_T_slack + l_MT(t))*v_MT(t)/(v_M_max*sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)) + a(t)*FiberForceLengthActiveDeGroote2016(sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)/l_M_opt, 0.814, 1.06, 0.162, 0.0633, 0.433, 0.717, -0.0299, 0.2, 0.1, 1.0, 0.354, 0.0)*FiberForceVelocityDeGroote2016((-l_T_slack + l_MT(t))*v_MT(t)/(v_M_max*sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)), -0.318, -8.149, -0.374, 0.886) + FiberForceLengthPassiveDeGroote2016(sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)/l_M_opt, 0.6, 4.0))
SymPy 在 MusculotendonDeGroote2016 类中提供了这种刚性肌腱动力学的实现,下面将展示一个完整的演示,我们将构建一个完整的简单肌腱模型。
弹性肌腱动力学¶
弹性肌腱动力学更为复杂,因为我们无法直接用肌腱长度来表示纤维长度,因为肌腱长度是变化的。相反,我们必须将肌腱中所承受的力与肌肉纤维产生的力联系起来,确保两者处于平衡状态。我们无法在不引入肌腱动力学中的另一个状态变量的情况下做到这一点,因此需要另一个一阶常微分方程。对于这个状态,我们可以有很多选择,但也许最直观的之一是使用 \(\tilde{l}^M\)。这样一来,我们需要同时为肌腱力 (\(F^T\)) 和 \(\frac{d \tilde{l}^M}{dt}\) 的一阶常微分方程创建表达式。 \(l^M\)、\(l^T\) 和 \(\tilde{l}^T\) 可以类似于刚性肌腱动力学来计算,请记住,我们已经有了 \(\tilde{l}^M\),因为它是一个状态变量。
使用 \(\tilde{l}^T\) 和肌腱力-长度曲线 (\(fl^T\left(\tilde{l}^T\right)\)),我们可以写出归一化和绝对肌腱力的方程
为了表达 \(F^M\),我们需要知道羽化角的余弦 (\(\cos{\alpha}\))。我们可以使用三角函数来写出它的方程
如果我们假设阻尼系数 \(\beta = 0\),我们可以重新排列肌肉纤维力方程
得到 \(fv^M\left(\tilde{v}^M\right)\)
使用反向纤维力-速度曲线 \(\left[fv^M\left(\tilde{v}^M\right)\right]^{-1}\),并将 \(\tilde{l}^M\) 对时间求导,我们终于可以写出 \(\frac{d \tilde{l}^M}{dt}\) 的方程
为了制定这些弹性肌腱肌腱动力学,我们不得不假设 \(\beta = 0\),这在正向模拟和最优控制问题中是不理想的。可以制定带有阻尼的弹性肌腱肌腱动力学,但这需要更复杂的公式,除了一个额外的状态变量之外还需要一个额外的输入变量,因此肌腱动力学必须作为微分代数方程而不是常微分方程来执行。这里不会讨论这些类型的公式的具体细节,但感兴趣的读者可以参考 MusculotendonDeGroote2016 的文档字符串,其中实现了这些公式。
一个简单的肌腱模型¶
为了演示肌肉对简单系统的影響,我们可以模拟一个质量为 \(m\) 的粒子在重力的作用下,肌肉拉动粒子对抗重力。质量 \(m\) 只有一个广义坐标 \(q\) 和广义速度 \(u\) 来描述它的位置和运动。以下代码建立了运动学和重力以及相关的粒子
>>> import pprint
>>> import sympy as sm
>>> import sympy.physics.mechanics as me
>>> q, u = me.dynamicsymbols('q, u', real=True)
>>> m, g = sm.symbols('m, g', real=True, positive=True)
>>> N = me.ReferenceFrame('N')
>>> O, P = sm.symbols('O, P', cls=me.Point)
>>> P.set_pos(O, q*N.x)
>>> O.set_vel(N, 0)
>>> P.set_vel(N, u*N.x)
>>> gravity = me.Force(P, m*g*N.x)
>>> block = me.Particle('block', P, m)
SymPy 生物力学包含肌腱执行器模型。在这里,我们将使用一个特定的肌腱模型实现。肌腱执行器使用两个输入组件实例化,即路径和激活动力学模型。执行器必须沿着连接肌肉起点和插入点的路径作用。我们的起点将连接到固定点 \(O\),并插入到移动粒子 \(P\) 上。
>>> from sympy.physics.mechanics.pathway import LinearPathway
>>> muscle_pathway = LinearPathway(O, P)
一条路径有两个连接点
>>> muscle_pathway.attachments
(O, P)
并且知道两个端点之间的长度以及两个端点之间的相对速度
>>> muscle_pathway.length
Abs(q(t))
>>> muscle_pathway.extension_velocity
sign(q(t))*Derivative(q(t), t)
最后,路径可以确定作用在两个连接点上的力,给定一个力的幅度
>>> muscle_pathway.to_loads(m*g)
[(O, - g*m*q(t)/Abs(q(t))*N.x), (P, g*m*q(t)/Abs(q(t))*N.x)]
激活动力学模型表示一组代数或常微分方程,这些方程将肌肉兴奋与肌肉激活联系起来。在本例中,我们将使用一阶常微分方程,它从激励 \(e(t)\) 给出一个平滑但延迟的激活 \(a(t)\)。
>>> from sympy.physics.biomechanics import FirstOrderActivationDeGroote2016
>>> muscle_activation = FirstOrderActivationDeGroote2016.with_defaults('muscle')
激活模型有一个状态变量 \(\mathbf{x}\)、一个输入变量 \(\mathbf{r}\) 和一些常数参数 \(\mathbf{p}\)
>>> muscle_activation.x
Matrix([[a_muscle(t)]])
>>> muscle_activation.r
Matrix([[e_muscle(t)]])
>>> muscle_activation.p
Matrix(0, 1, [])
请注意,常数参数的返回值为空。如果我们像往常一样实例化 FirstOrderActivationDeGroote2016,那么我们必须提供三个值,分别为 \(\tau_{a}\)、\(\tau_{d}\) 和 \(b\)。如果这些是 Symbol 对象,那么它们将出现在返回的 MutableDenseMatrix 中。
这些与它的一个一阶常微分方程 \(\dot{a} = f(a, e, t)\) 相关联
>>> muscle_activation.rhs()
Matrix([[((1/2 - tanh(10.0*a_muscle(t) - 10.0*e_muscle(t))/2)/(0.0225*a_muscle(t) + 0.0075) + 16.6666666666667*(3*a_muscle(t)/2 + 1/2)*(tanh(10.0*a_muscle(t) - 10.0*e_muscle(t))/2 + 1/2))*(-a_muscle(t) + e_muscle(t))]])
有了路径和激活动力学,使用这两者创建的肌腱模型需要一些参数来定义肌肉和肌腱的特定属性。您需要指定肌腱松弛长度、峰值等长力、最佳纤维长度、最大纤维速度、最佳羽化角和纤维阻尼系数。
>>> from sympy.physics.biomechanics import MusculotendonDeGroote2016
>>> F_M_max, l_M_opt, l_T_slack = sm.symbols('F_M_max, l_M_opt, l_T_slack', real=True)
>>> v_M_max, alpha_opt, beta = sm.symbols('v_M_max, alpha_opt, beta', real=True)
>>> muscle = MusculotendonDeGroote2016.with_defaults(
... 'muscle',
... muscle_pathway,
... muscle_activation,
... tendon_slack_length=l_T_slack,
... peak_isometric_force=F_M_max,
... optimal_fiber_length=l_M_opt,
... maximal_fiber_velocity=v_M_max,
... optimal_pennation_angle=alpha_opt,
... fiber_damping_coefficient=beta,
... )
...
因为这个肌腱执行器有一个刚性肌腱模型,所以它与激活模型具有相同的状态和常微分方程
>>> muscle.musculotendon_dynamics
0
>>> muscle.x
Matrix([[a_muscle(t)]])
>>> muscle.r
Matrix([[e_muscle(t)]])
>>> muscle.p
Matrix([
[l_T_slack],
[ F_M_max],
[ l_M_opt],
[ v_M_max],
[alpha_opt],
[ beta]])
>>> muscle.rhs()
Matrix([[((1/2 - tanh(10.0*a_muscle(t) - 10.0*e_muscle(t))/2)/(0.0225*a_muscle(t) + 0.0075) + 16.6666666666667*(3*a_muscle(t)/2 + 1/2)*(tanh(10.0*a_muscle(t) - 10.0*e_muscle(t))/2 + 1/2))*(-a_muscle(t) + e_muscle(t))]])
肌腱提供了额外的常微分方程以及作用于路径的肌肉特异性力
>>> muscle_loads = muscle.to_loads()
>>> pprint.pprint(muscle_loads)
[Force(point=O, force=F_M_max*(beta*(-l_T_slack + Abs(q(t)))*sign(q(t))*Derivative(q(t), t)/(v_M_max*sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + Abs(q(t)))**2)) + a_muscle(t)*FiberForceLengthActiveDeGroote2016(sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + Abs(q(t)))**2)/l_M_opt, 0.814, 1.06, 0.162, 0.0633, 0.433, 0.717, -0.0299, 0.2, 0.1, 1.0, 0.354, 0.0)*FiberForceVelocityDeGroote2016((-l_T_slack + Abs(q(t)))*sign(q(t))*Derivative(q(t), t)/(v_M_max*sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + Abs(q(t)))**2)), -0.318, -8.149, -0.374, 0.886) + FiberForceLengthPassiveDeGroote2016(sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + Abs(q(t)))**2)/l_M_opt, 0.6, 4.0))*q(t)*cos(alpha_opt)/Abs(q(t))*N.x),
Force(point=P, force=- F_M_max*(beta*(-l_T_slack + Abs(q(t)))*sign(q(t))*Derivative(q(t), t)/(v_M_max*sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + Abs(q(t)))**2)) + a_muscle(t)*FiberForceLengthActiveDeGroote2016(sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + Abs(q(t)))**2)/l_M_opt, 0.814, 1.06, 0.162, 0.0633, 0.433, 0.717, -0.0299, 0.2, 0.1, 1.0, 0.354, 0.0)*FiberForceVelocityDeGroote2016((-l_T_slack + Abs(q(t)))*sign(q(t))*Derivative(q(t), t)/(v_M_max*sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + Abs(q(t)))**2)), -0.318, -8.149, -0.374, 0.886) + FiberForceLengthPassiveDeGroote2016(sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + Abs(q(t)))**2)/l_M_opt, 0.6, 4.0))*q(t)*cos(alpha_opt)/Abs(q(t))*N.x)]
这些载荷由描述长度和速度关系与肌肉纤维力的各种函数组成。
现在我们有了肌肉和肌腱产生的力,系统的运动方程可以用例如凯恩方法来形成
>>> kane = me.KanesMethod(N, (q,), (u,), kd_eqs=(u - q.diff(),))
>>> Fr, Frs = kane.kanes_equations((block,), (muscle_loads + [gravity]))
运动方程由运动学微分方程、动力学微分方程(牛顿第二定律)和肌肉激活微分方程组成。每个方程的显式形式可以这样形成
>>> dqdt = u
>>> dudt = kane.forcing[0]/m
>>> dadt = muscle.rhs()[0]
现在,我们可以创建一个数值函数,在给定状态、输入和常数参数的情况下评估运动方程。首先,列出每个符号
>>> a = muscle.a
>>> e = muscle.e
>>> state = [q, u, a]
>>> inputs = [e]
>>> constants = [m, g, F_M_max, l_M_opt, l_T_slack, v_M_max, alpha_opt, beta]
然后,评估显式常微分方程右边的数值函数为
>>> eval_eom = sm.lambdify((state, inputs, constants), (dqdt, dudt, dadt))
此外,数值评估肌肉力也很有意思,因此也创建一个函数
>>> force = muscle.force.xreplace({q.diff(): u})
>>> eval_force = sm.lambdify((state, constants), force)
为了测试这些函数,我们需要一些合适的数值。这块肌肉能够产生 10 N 的最大力来抬起 0.5 kg 的质量
>>> import numpy as np
>>> p_vals = np.array([
... 0.5, # m [kg]
... 9.81, # g [m/s/s]
... 10.0, # F_M_max [N]
... 0.18, # l_M_opt [m]
... 0.17, # l_T_slack [m]
... 10.0, # v_M_max [m/s]
... 0.0, # alpha_opt
... 0.1, # beta
... ])
...
我们的肌腱是刚性的,因此肌肉的长度将是 \(q-l_{T_\textrm{slack}}\),我们想要给出一个接近其力产生峰值的初始肌肉长度,所以我们选择 \(q_0=l_{M_\textrm{opt}} + l_{T_\textrm{slack}}\)。让我们也给肌肉一个小的初始激活,这样它就能产生一个非零的力
>>> x_vals = np.array([
... p_vals[3] + p_vals[4], # q [m]
... 0.0, # u [m/s]
... 0.1, # a [unitless]
... ])
...
将激励设置为 1.0 并测试数值函数
>>> r_vals = np.array([
... 1.0, # e
... ])
...
>>> eval_eom(x_vals, r_vals, p_vals)
(0.0, 7.817106179880225, 92.30769105034035)
>>> eval_force(x_vals, p_vals)
-0.9964469100598874
这两个函数都起作用,所以我们现在可以模拟这个系统,看看肌肉是否以及如何举起质量
>>> def eval_rhs(t, x):
...
... r = np.array([1.0])
...
... return eval_eom(x, r, p_vals)
...
>>> from scipy.integrate import solve_ivp
>>> t0, tf = 0.0, 6.0
>>> times = np.linspace(t0, tf, num=601)
>>> sol = solve_ivp(eval_rhs,
... (t0, tf),
... x_vals, t_eval=times)
...
>>> import matplotlib.pyplot as plt
>>> fig, axes = plt.subplots(4, 1, sharex=True)
>>> _ = axes[0].plot(sol.t, sol.y[0] - p_vals[4], label='length of muscle')
>>> _ = axes[0].set_ylabel('Distance [m]')
>>> _ = axes[1].plot(sol.t, sol.y[1], label=state[1])
>>> _ = axes[1].set_ylabel('Speed [m/s]')
>>> _ = axes[2].plot(sol.t, sol.y[2], label=state[2])
>>> _ = axes[2].set_ylabel('Activation')
>>> _ = axes[3].plot(sol.t, eval_force(sol.y, p_vals).T, label='force')
>>> _ = axes[3].set_ylabel('Force [N]')
>>> _ = axes[3].set_xlabel('Time [s]')
>>> _ = axes[0].legend(), axes[1].legend(), axes[2].legend(), axes[3].legend()
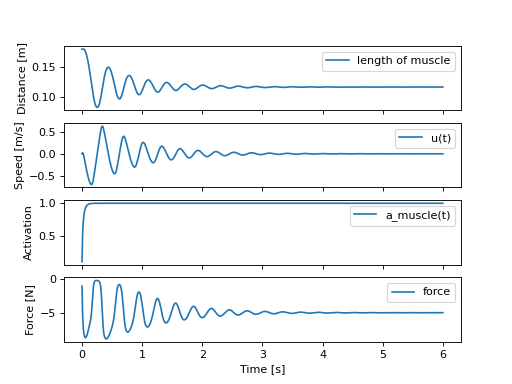
肌肉拉动质量,与重力相反,并衰减到 5 N 的平衡状态。