代数解常微分方程 (ODE)

使用 SymPy 代数解常微分方程 (ODE)。例如，解 \(y''(x) + 9y(x)=0 \) 得到 \( y(x)=C_{1} \sin(3x)+ C_{2} \cos(3x)\).

其他方案

• 要数值求解 ODE 组，请使用 SciPy ODE 求解器，例如 solve_ivp。您也可以使用 SymPy 创建 ODE，然后使用 lambdify() 将其数值求解，如以下 SciPy 中的数值解 ODE 所述。

解常微分方程 (ODE)

以下示例使用 dsolve() 代数解上述常微分方程。然后可以使用 checkodesol() 验证解是否正确。

>>> from sympy import Function, dsolve, Derivative, checkodesol
>>> from sympy.abc import x
>>> y = Function('y')
>>> # Solve the ODE
>>> result = dsolve(Derivative(y(x), x, x) + 9*y(x), y(x))
>>> result
Eq(y(x), C1*sin(3*x) + C2*cos(3*x))
>>> # Check that the solution is correct
>>> checkodesol(Derivative(y(x), x, x) + 9*y(x), result)
(True, 0)

checkodesol() 的输出是一个元组，其中第一个元素是布尔值，表示将解代入 ODE 后是否得到 0，表示解是正确的。

指南

定义导数

有多种方法可以表达函数的导数。对于未定义的函数，Derivative 和 diff() 都表示未定义的导数。因此，以下所有 ypp（“y prime prime”）都代表 \(y''\)，即函数 \(y(x)\) 对 \(x\) 的二阶导数

ypp = y(x).diff(x, x)
ypp = y(x).diff(x, 2)
ypp = y(x).diff((x, 2))
ypp = diff(y(x), x, x)
ypp = diff(y(x), x, 2)
ypp = Derivative(y(x), x, x)
ypp = Derivative(y(x), x, 2)
ypp = Derivative(Derivative(y(x), x), x)
ypp = diff(diff(y(x), x), x)
yp = y(x).diff(x)
ypp = yp.diff(x)

我们建议将要求解的函数作为 dsolve() 的第二个参数指定。注意，它必须是函数而不是变量（符号）。如果指定了变量（\(x\)）而不是函数（\(f(x)\)），SymPy 将会报错

>>> dsolve(Derivative(y(x), x, x) + 9*y(x), x)
Traceback (most recent call last):
    ...
ValueError: dsolve() and classify_ode() only work with functions of one variable, not x

同样，您必须指定函数的参数：\(y(x)\)，而不仅仅是 \(y\)。

定义 ODE 的选项

您可以通过两种方式定义要求解的函数。后续指定初始条件的语法取决于您的选择。

选项 1：在不包含其自变量的情况下定义函数

您可以在不包含其自变量的情况下定义函数

>>> from sympy import symbols, Eq, Function, dsolve
>>> f, g = symbols("f g", cls=Function)
>>> x = symbols("x")
>>> eqs = [Eq(f(x).diff(x), g(x)), Eq(g(x).diff(x), f(x))]
>>> dsolve(eqs, [f(x), g(x)])
[Eq(f(x), -C1*exp(-x) + C2*exp(x)), Eq(g(x), C1*exp(-x) + C2*exp(x))]

请注意，您将要求解的函数作为 dsolve() 的第二个参数提供，此处为 [f(x), g(x)]。

指定初始条件或边界条件

如果您的微分方程（组）具有初始条件或边界条件，请使用 dsolve() 的可选参数 ics 指定它们。初始条件和边界条件的处理方式相同（即使参数名为 ics）。它应该以 {f(x0): y0, f(x).diff(x).subs(x, x1): y1} 等等的形式给出，例如，\(f(x)\) 在 \(x = x_{0}\) 处的值为 \(y_{0}\)。对于幂级数解，如果未指定初始条件，则假设 \(f(0)\) 为 \(C_{0}\)，并计算关于 \(0\) 的幂级数解。

以下是如何为函数设置初始值的示例，即 \(f(0) = 1\) 和 \(g(2) = 3\)

>>> from sympy import symbols, Eq, Function, dsolve
>>> f, g = symbols("f g", cls=Function)
>>> x = symbols("x")
>>> eqs = [Eq(f(x).diff(x), g(x)), Eq(g(x).diff(x), f(x))]
>>> dsolve(eqs, [f(x), g(x)])
[Eq(f(x), -C1*exp(-x) + C2*exp(x)), Eq(g(x), C1*exp(-x) + C2*exp(x))]
>>> dsolve(eqs, [f(x), g(x)], ics={f(0): 1, g(2): 3})
[Eq(f(x), (1 + 3*exp(2))*exp(x)/(1 + exp(4)) - (-exp(4) + 3*exp(2))*exp(-x)/(1 + exp(4))), Eq(g(x), (1 + 3*exp(2))*exp(x)/(1 + exp(4)) + (-exp(4) + 3*exp(2))*exp(-x)/(1 + exp(4)))]

以下是如何为函数的导数设置初始值的示例，即 \(f'(1) = 2\)

>>> eqn = Eq(f(x).diff(x), f(x))
>>> dsolve(eqn, f(x), ics={f(x).diff(x).subs(x, 1): 2})
Eq(f(x), 2*exp(-1)*exp(x))

选项 2：定义自变量的函数

您可能更喜欢指定一个函数（例如 \(y\)）及其自变量（例如 \(t\)），以便 y 代表 y(t)

>>> from sympy import symbols, Function, dsolve
>>> t = symbols('t')
>>> y = Function('y')(t)
>>> y
y(t)
>>> yp = y.diff(t)
>>> ypp = yp.diff(t)
>>> eq = ypp + 2*yp + y
>>> eq
y(t) + 2*Derivative(y(t), t) + Derivative(y(t), (t, 2))
>>> dsolve(eq, y)
Eq(y(t), (C1 + C2*t)*exp(-t))

使用此约定，dsolve() 的第二个参数 y 代表 y(t)，因此 SymPy 会将其识别为一个有效的要求解的函数。

指定初始条件或边界条件

使用该语法，您可以通过使用 subs() 代入自变量的值来指定初始条件或边界条件，因为函数 \(y\) 已经将自变量作为参数 \(t\)

>>> dsolve(eq, y, ics={y.subs(t, 0): 0})
Eq(y(t), C2*t*exp(-t))

注意复制和粘贴结果

如果您选择定义自变量的函数，请注意，复制结果并将其粘贴到后续代码中可能会导致错误，因为 x 已经定义为 y(t)，因此，如果您粘贴了 y(t)，它将被解释为 y(t)(t)

>>> dsolve(y(t).diff(y), y)
Traceback (most recent call last):
    ...
TypeError: 'y' object is not callable

因此，请记住省略自变量调用 (t)

>>> dsolve(y.diff(t), y)
Eq(y(t), C1)

使用解结果

与其他求解函数不同，dsolve() 返回一个 Equality（方程），其格式为，例如，Eq(y(x), C1*sin(3*x) + C2*cos(3*x))，它等效于数学表示法 \(y(x) = C_1 \sin(3x) + C_2 \cos(3x)\)。

提取一个解和函数的结果

您可以使用右手侧属性 rhs 从 Equality 中提取结果

>>> from sympy import Function, dsolve, Derivative
>>> from sympy.abc import x
>>> y = Function('y')
>>> result = dsolve(Derivative(y(x), x, x) + 9*y(x), y(x))
>>> result
Eq(y(x), C1*sin(3*x) + C2*cos(3*x))
>>> result.rhs
C1*sin(3*x) + C2*cos(3*x)

有些 ODE 无法显式求解，只能隐式求解

以上 ODE 可以显式求解，具体来说，可以根据 \(x\) 的函数来表达 \(y(x)\)。但是，有些 ODE 无法显式求解，例如

>>> from sympy import dsolve, exp, symbols, Function
>>> f = symbols("f", cls=Function)
>>> x = symbols("x")
>>> dsolve(f(x).diff(x) + exp(-f(x))*f(x))
Eq(Ei(f(x)), C1 - x)

这没有直接给出 \(f(x)\) 的表达式。相反，dsolve() 将解表达为 \(g(f(x))\)，其中 \(g\) 为 Ei，即经典指数积分函数。Ei 没有已知的封闭形式逆函数，因此无法将解显式表达为 \(f(x)\) 等于 \(x\) 的函数。相反，dsolve 返回一个 隐式解。

当 dsolve 返回一个隐式解时，提取返回的等式的右手侧将不会给出要求解的函数（此处为 \(f(x)\)）的显式表达式。因此，在提取要求解的函数的表达式之前，请检查 dsolve 是否能够显式求解该函数。

提取多个函数-解对的结果

如果您正在求解具有多个未知函数的方程组，则 dsolve() 的输出形式取决于是否存在一个或多个解。

如果存在一个解集

如果具有多个未知函数的方程组只有一个解集，dsolve() 将返回一个包含等式的非嵌套列表。您可以使用单个循环或推导来提取解表达式

>>> from sympy import symbols, Eq, Function, dsolve
>>> y, z = symbols("y z", cls=Function)
>>> x = symbols("x")
>>> eqs_one_soln_set = [Eq(y(x).diff(x), z(x)**2), Eq(z(x).diff(x), z(x))]
>>> solutions_one_soln_set = dsolve(eqs_one_soln_set, [y(x), z(x)])
>>> solutions_one_soln_set
[Eq(y(x), C1 + C2**2*exp(2*x)/2), Eq(z(x), C2*exp(x))]
>>> # Loop through list approach
>>> solution_one_soln_set_dict = {}
>>> for fn in solutions_one_soln_set:
...         solution_one_soln_set_dict.update({fn.lhs: fn.rhs})
>>> solution_one_soln_set_dict
{y(x): C1 + C2**2*exp(2*x)/2, z(x): C2*exp(x)}
>>> # List comprehension approach
>>> solution_one_soln_set_dict = {fn.lhs:fn.rhs for fn in solutions_one_soln_set}
>>> solution_one_soln_set_dict
{y(x): C1 + C2**2*exp(2*x)/2, z(x): C2*exp(x)}
>>> # Extract expression for y(x)
>>> solution_one_soln_set_dict[y(x)]
C1 + C2**2*exp(2*x)/2

如果存在多个解集

如果具有多个未知函数的方程组存在多个解集，dsolve() 将返回一个嵌套的等式列表，外层列表代表每个解，内层列表代表每个函数。虽然您可以通过指定每个函数的索引来提取结果，但我们建议使用一种方法，该方法对函数排序是健壮的。以下方法将每个解转换为字典，因此您可以轻松地提取所需函数的结果。它使用了标准的 Python 技术，例如循环或推导，以嵌套方式。

>>> from sympy import symbols, Eq, Function, dsolve
>>> y, z = symbols("y z", cls=Function)
>>> x = symbols("x")
>>> eqs = [Eq(y(x).diff(x)**2, z(x)**2), Eq(z(x).diff(x), z(x))]
>>> solutions = dsolve(eqs, [y(x), z(x)])
>>> solutions
[[Eq(y(x), C1 - C2*exp(x)), Eq(z(x), C2*exp(x))], [Eq(y(x), C1 + C2*exp(x)), Eq(z(x), C2*exp(x))]]
>>> # Nested list approach
>>> solutions_list = []
>>> for solution in solutions:
...     solution_dict = {}
...     for fn in solution:
...             solution_dict.update({fn.lhs: fn.rhs})
...     solutions_list.append(solution_dict)
>>> solutions_list
[{y(x): C1 - C2*exp(x), z(x): C2*exp(x)}, {y(x): C1 + C2*exp(x), z(x): C2*exp(x)}]
>>> # Nested comprehension approach
>>> solutions_list = [{fn.lhs:fn.rhs for fn in solution} for solution in solutions]
>>> solutions_list
[{y(x): C1 - C2*exp(x), z(x): C2*exp(x)}, {y(x): C1 + C2*exp(x), z(x): C2*exp(x)}]
>>> # Extract expression for y(x)
>>> solutions_list[0][y(x)]
C1 - C2*exp(x)

处理任意常数

您可以操作任意常数，例如 C1、C2 和 C3，这些常数是由 dsolve() 自动生成的，方法是将它们创建为符号。例如，如果您想为任意常数赋值，您可以将它们创建为符号，然后使用 subs() 代入其值

>>> from sympy import Function, dsolve, Derivative, symbols, pi
>>> y = Function('y')
>>> x, C1, C2 = symbols("x, C1, C2")
>>> result = dsolve(Derivative(y(x), x, x) + 9*y(x), y(x)).rhs
>>> result
C1*sin(3*x) + C2*cos(3*x)
>>> result.subs({C1: 7, C2: pi})
7*sin(3*x) + pi*cos(3*x)

在 SciPy 中数值求解 ODE

利用 SciPy 的快速数值 ODE 求解的常见工作流程是

1. 在 SymPy 中设置 ODE

2. 使用 lambdify() 将其转换为数值函数。

3. 通过 使用 SciPy 的 solve_ivp 对 ODE 进行数值积分 来求解初值问题。

以下是一个来自 化学动力学领域 的示例，其中非线性常微分方程采用以下形式

\[\begin{split} r_f = & k_f y_0(t)^2 y_1(t) \\ r_b = & k_b y_2(t)^2 \\ \frac{d y_0(t)}{dt} = & 2(r_b - r_f) \\ \frac{d y_1(t)}{dt} = & r_b - r_f \\ \frac{d y_2(t)}{dt} = & 2(r_f - r_b) \end{split}\]

以及

\[\begin{split}\vec{y}(t) = \begin{bmatrix} y_0(t) \\ y_1(t) \\ y_2(t) \end{bmatrix} \end{split}\]

>>> from sympy import symbols, lambdify
>>> import numpy as np
>>> import scipy.integrate
>>> import matplotlib.pyplot as plt
>>> # Create symbols y0, y1, and y2
>>> y = symbols('y:3')
>>> kf, kb = symbols('kf kb')
>>> rf = kf * y[0]**2 * y[1]
>>> rb = kb * y[2]**2
>>> # Derivative of the function y(t); values for the three chemical species
>>> # for input values y, kf, and kb
>>> ydot = [2*(rb - rf), rb - rf, 2*(rf - rb)]
>>> ydot
[2*kb*y2**2 - 2*kf*y0**2*y1, kb*y2**2 - kf*y0**2*y1, -2*kb*y2**2 + 2*kf*y0**2*y1]
>>> t = symbols('t') # not used in this case
>>> # Convert the SymPy symbolic expression for ydot into a form that
>>> # SciPy can evaluate numerically, f
>>> f = lambdify((t, y, kf, kb), ydot)
>>> k_vals = np.array([0.42, 0.17]) # arbitrary in this case
>>> y0 = [1, 1, 0] # initial condition (initial values)
>>> t_eval = np.linspace(0, 10, 50) # evaluate integral from t = 0-10 for 50 points
>>> # Call SciPy's ODE initial value problem solver solve_ivp by passing it
>>> #   the function f,
>>> #   the interval of integration,
>>> #   the initial state, and
>>> #   the arguments to pass to the function f
>>> solution = scipy.integrate.solve_ivp(f, (0, 10), y0, t_eval=t_eval, args=k_vals)
>>> # Extract the y (concentration) values from SciPy solution result
>>> y = solution.y
>>> # Plot the result graphically using matplotlib
>>> plt.plot(t_eval, y.T) 
>>> # Add title, legend, and axis labels to the plot
>>> plt.title('Chemical Kinetics') 
>>> plt.legend(['NO', 'Br$_2$', 'NOBr'], shadow=True) 
>>> plt.xlabel('time') 
>>> plt.ylabel('concentration') 
>>> # Finally, display the annotated plot
>>> plt.show()

(png, hires.png, pdf)

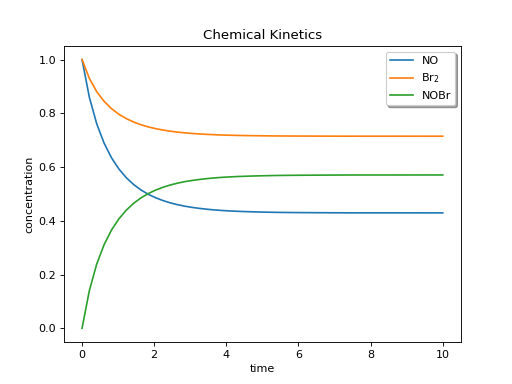
SciPy 的 solve_ivp 返回一个结果，包含 y（数值函数结果，此处为浓度）值，对应于三个化学物质中的每一个，对应于时间点 t_eval。

常微分方程求解提示

返回未计算的积分

默认情况下，dsolve() 尝试计算它为求解常微分方程而生成的积分。您可以使用以 _Integral 结尾的 提示函数 来禁用积分的计算，例如 separable_Integral。这是有用的，因为 integrate() 是一个昂贵的例程。SymPy 可能由于困难或无法计算的积分而挂起（似乎永远无法完成操作），因此使用 _Integral 提示至少会返回一个（未积分的）结果，您可以考虑该结果。禁用积分的最简单方法是使用 all_Integral 提示，因为您不需要知道要提供哪个提示：对于具有对应 _Integral 提示的任何提示，all_Integral 只返回 _Integral 提示。

选择特定的求解器

出于以下几个原因，您可能希望使用提示选择特定的求解器

• 教育目的：例如，如果您正在学习特定方法来求解 ODE，并且想要获得与该方法完全匹配的结果

• 结果的形式：有时，ODE 可以通过多种不同的求解器来求解，并且它们可以返回不同的结果。它们在数学上是等价的，尽管任意常数可能不同。 dsolve() 默认情况下尝试首先使用“最佳”求解器，这些求解器最有可能返回最易用的输出，但这并不是一个完美的启发式方法。例如，“最佳”求解器可能会产生一个具有 SymPy 无法求解的积分的结果，而另一个求解器可能会产生一个 SymPy 可以求解的不同积分。因此，如果解决方案不是您喜欢的形式，您可以尝试其他提示以查看它们是否会给出更可取的结果。

并非所有方程都能求解

无解的方程

并非所有微分方程都能求解，例如

>>> from sympy import Function, dsolve, Derivative, symbols
>>> y = Function('y')
>>> x, C1, C2 = symbols("x, C1, C2")
>>> dsolve(Derivative(y(x), x, 3) - (y(x)**2), y(x)).rhs
Traceback (most recent call last):
    ...
NotImplementedError: solve: Cannot solve -y(x)**2 + Derivative(y(x), (x, 3))

无封闭形式解的方程

如上所述，有些 ODE 无法显式求解，只能隐式求解。

此外，一些微分方程组没有封闭形式的解，因为它们是混沌的，例如 洛伦茨系统 或由以下两个微分方程描述的双摆（简化自 ScienceWorld）

\[ 2 \theta_1''(t) + \theta_2''(t) \cos(\theta_1-\theta_2) + \theta_2'^2(t) \sin(\theta_1 - \theta_2) + 2g \sin(\theta_1) = 0 \]

\[ \theta_2''(t) + \theta_1''(t) \cos(\theta_1-\theta_2) - \theta_1'^2(t) \sin(\theta_1 - \theta_2) + g \sin(\theta_2) = 0 \]

>>> from sympy import symbols, Function, cos, sin, dsolve
>>> theta1, theta2 = symbols('theta1 theta2', cls=Function)
>>> g, t = symbols('g t')
>>> eq1 = 2*theta1(t).diff(t, t) + theta2(t).diff(t, t)*cos(theta1(t) - theta2(t)) + theta2(t).diff(t)**2*sin(theta1(t) - theta2(t)) + 2*g*sin(theta1(t))
>>> eq2 = theta2(t).diff(t, t) + theta1(t).diff(t, t)*cos(theta1(t) - theta2(t)) - theta1(t).diff(t)**2*sin(theta1(t) - theta2(t)) + g*sin(theta2(t))
>>> dsolve([eq1, eq2], [theta1(t), theta2(t)])
Traceback (most recent call last):
...
NotImplementedError

对于此类情况，您可以像在 其他方法 中提到的那样对方程进行数值求解。

报告错误

如果您发现 dsolve() 存在错误，请在 SymPy 邮件列表 上发布问题。在问题解决之前，您可以使用 其他方法 中列出的其他方法。